Ramblings on Variation

Following on from MathsConf15 and Mr Barton's workshop, I’ve played around a little bit more with variation theory.

Previously, I’ve experimented lots with concrete, pictorial and abstract conceptual variation, and have found what works for me. Procedural variation is something I’ve not done much work on in the past.

Courtesy of Jurassic Maths Hub

Procedural variation is used to support pupils' deeper understanding of a mathematical procedure or process. This might be to compare the same procedure used to calculate two different sets of numbers by asking the pupils to compare two successive procedures where the first is linked to a second. Hopefully they will observe relationships, observe the variant and invariant properties of the procedure, leading to generalising about the procedure.

When done well, procedural variation provides the opportunity for intelligent rather than mechanical practice and, by making connections, students should be able to form conjectures about what answers might be to slightly varied questions. If you like lots of discussion in your classroom, this is a great way to get students talking about maths rather than what they did at the weekend (this usually happens with mind-numbing tasks where students only need to do minimal thinking).

There are shed-loads of variation tasks available at Variation Theory (created and collated by Craig Barton, Jess Prior and Ben Gordan) and I’ve used several of the tasks from Minimally Different Exercises, but I knew I needed to work on delivery of these tasks.

Following the workshop at the weekend, I’ve taught two lessons using these resources. They’re not appropriate to use every lesson (much to my year 9s’ disappointment today!) as students still need scaffolding, questioning, exam practice, rich tasks and so much more. As Craig said in his workshop, this is a part of a diet of maths, an important part however, but just a part.

I had tried hard to get students thinking and talking about the variation from question to question when using these resources in the last month or so, but it still felt like too much of an ‘opt-in or opt-out’ kind of task. I needed something to explicitly make students reflect and expect before calculating what the answer to each question was. So I’ve put together a couple of worksheets. The questions are all from Variation Theory, it’s only the structure that I’ve played around with.

After the first lesson on prime factorisation, I toyed with the idea of removing the reflect column. My students had struggled with getting their reflective thoughts down onto paper. I felt I had done a lot of the work for them and wondered whether the reflect column was worth it. After raising my thoughts on Twitter, Rob Smith urged me to continue to get students to fill it in; “Just because it is hard (at the minute) persevere! They will be better students for it!” He’s right of course.

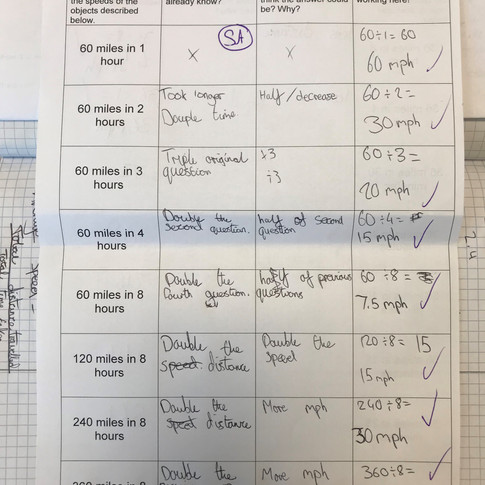
A second lesson today on speed, distance and time with a more cooperative class supported that conversation. We filled in the first three rows of the sheet as a group, focusing on questioning, vocabulary and arithmetic. Once students had a clear example of links they could make, they were far more confident with the task. Several students got ‘stuck’ at points because they didn’t know what to expect. I reassured them and watched the lightbulb moment as they went straight to the check column and saw a clear connection with earlier questions.

I’m hopeful that, with a little training, this will definitely support my students in having a much deeper understanding of maths. I asked my students what they thought at the end of today’s lesson, and some of the comments were as follows:

• “I don’t think I’ll forget it now”;

• “It made me think”;

• “I had to work harder” (this is my favourite!); and

• “You couldn’t just do the same thing”.

I asked the last student to elaborate further and he explained that usually, once he understands the method, every question was pretty much the same. Even though these questions were even more similar than usual, he was forced into spotting differences and similarities.

At the end of the speed, distance and time lesson, I asked students to generalise what they had found today. Unfortunately, this was too much too soon! I scaffolded it a little bit but writing four sentence (below) and asking them to fill in the gaps. Again, the conversation around the room was brilliant – all students were able to use the questions that they had completed to be able to justify their thoughts, and we were able to speak a little about inverse functions and reciprocals just before the bell.

I’ve always enjoyed trying new things in the classroom, I don’t think I’ll ever stop, but this is definitely the best thing I’ve tried for a while in terms of student progress and I’m looking forward to developing it further.

#maths #mathsteaching #variation #mathsconf15 #proceduralvariation #variationtheory #minimallydifferentquestions #speed #primefactorisation